In this article, you will learn how a transformer converts input tokens into context-aware representations and, ultimately, next-token probabilities.
Topics we will cover include:
- How tokenization, embeddings, and positional information prepare inputs
- What multi-headed attention and feed-forward networks contribute inside each layer
- How the final projection and softmax produce next-token probabilities
Let’s get our journey underway.
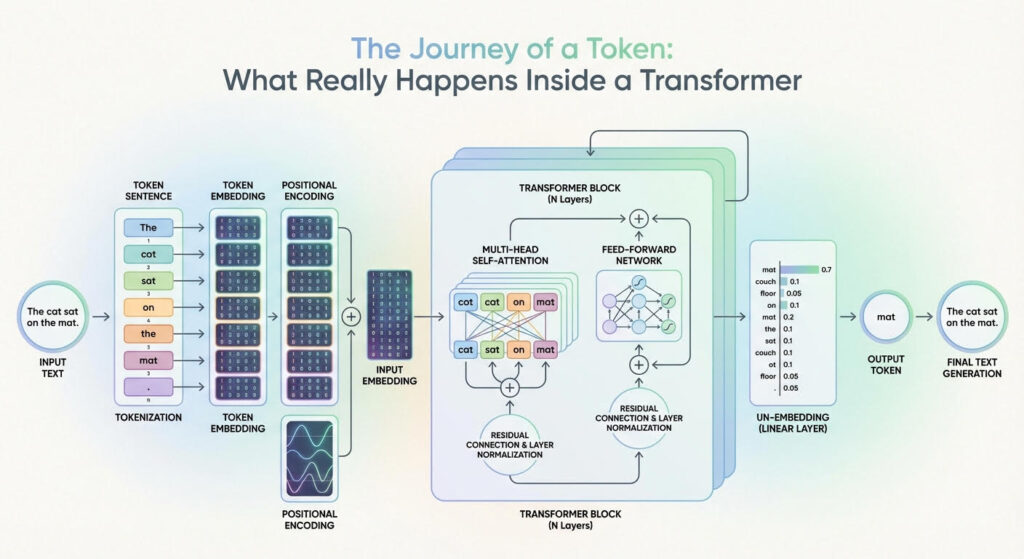
The Journey of a Token: What Really Happens Inside a Transformer (click to enlarge)
Image by Editor
The Journey Begins
Large language models (LLMs) are based on the transformer architecture, a complex deep neural network whose input is a sequence of token embeddings. After a deep process — that looks like a parade of numerous stacked attention and feed-forward transformations — it outputs a probability distribution that indicates which token should be generated next as part of the model’s response. But how can this journey from inputs to outputs be explained for a single token in the input sequence?
In this article, you will learn what happens inside a transformer model — the architecture behind LLMs — at the token level. In other words, we will see how input tokens or parts of an input text sequence turn into generated text outputs, and the rationale behind the changes and transformations that take place inside the transformer.
The description of this journey through a transformer model will be guided by the above diagram that shows a generic transformer architecture and how information flows and evolves through it.
Entering the Transformer: From Raw Input Text to Input Embedding
Before entering the depths of the transformer model, a few transformations already happen to the text input, primarily so it is represented in a form that is fully understandable by the internal layers of the transformer.
Tokenization
The tokenizer is an algorithmic component typically working in symbiosis with the LLM’s transformer model. It takes the raw text sequence, e.g. the user prompt, and splits it into discrete tokens (often subword units or bytes, sometimes whole words), with each token in the source language being mapped to an identifier i.
Token Embeddings
There is a learned embedding table E with shape |V| × d (vocabulary size by embedding dimension). Looking up the identifiers for a sequence of length n yields an embedding matrix X with shape n × d. That is, each token identifier is mapped to a d-dimensional embedding vector that forms one row of X. Two embedding vectors will be similar to each other if they are associated with tokens that have similar meanings, e.g. king and emperor, or vice versa. Importantly, at this stage, each token embedding carries semantic and lexical information for that single token, without incorporating information about the rest of the sequence (at least not yet).
Positional Encoding
Before fully entering the core parts of the transformer, it is necessary to inject within each token embedding vector — i.e. inside each row of the embedding matrix X — information about the position of that token in the sequence. This is also called injecting positional information, and it is typically done with trigonometric functions like sine and cosine, although there are techniques based on learned positional embeddings as well. A nearly-residual component is summed to the previous embedding vector e_t associated with a token, as follows:
\[
x_t^{(0)} = e_t + p_{\text{pos}}(t)
\]
with p_pos(t) typically being a trigonometric-based function of the token position t in the sequence. As a result, an embedding vector that formerly encoded “what a token is” only now encodes “what the token is and where in the sequence it sits”. This is equivalent to the “input embedding” block in the above diagram.
Now, time to enter the depths of the transformer and see what happens inside!
Deep Inside the Transformer: From Input Embedding to Output Probabilities
Let’s explain what happens to each “enriched” single-token embedding vector as it goes through one transformer layer, and then zoom out to describe what happens across the entire stack of layers.
The formula
\[
h_t^{(0)} = x_t^{(0)}
\]
is used to denote a token’s representation at layer 0 (the first layer), whereas more generically we will use ht(l) to denote the token’s embedding representation at layer l.
Multi-headed Attention
The first major component inside each replicated layer of the transformer is the multi-headed attention. This is arguably the most influential component in the entire architecture when it comes to identifying and incorporating into each token’s representation a lot of meaningful information about its role in the entire sequence and its relationships with other tokens in the text, be it syntactic, semantic, or any other sort of linguistic relationship. Multiple heads in this so-called attention mechanism are each specialized in capturing different linguistic aspects and patterns in the token and the entire sequence it belongs to simultaneously.
The result of having a token representation ht(l) (with positional information injected a priori, don’t forget!) traveling through this multi-headed attention inside a layer is a context-enriched or context-aware token representation. By using residual connections and layer normalizations across the transformer layer, newly generated vectors become stabilized blends of their own previous representations and the multi-headed attention output. This helps improve coherence throughout the entire process, which is applied repeatedly across layers.
Feed-forward Neural Network
Next comes something relatively less complex: a few feed-forward neural network (FFN) layers. For instance, these can be per-token multilayer perceptrons (MLPs) whose goal is to further transform and refine the token features that are gradually being learned.
The main difference between the attention stage and this one is that attention mixes and incorporates, in each token representation, contextual information from across all tokens, but the FFN step is applied independently on each token, refining the contextual patterns already integrated to yield useful “knowledge” from them. These layers are also supplemented with residual connections and layer normalizations, and as a result of this process, we have at the end of a transformer layer an updated representation ht(l+1) that will become the input to the next transformer layer, thereby entering another multi-headed attention block.
The whole process is repeated as many times as the number of stacked layers defined in our architecture, thus progressively enriching the token embedding with more and more higher-level, abstract, and long-range linguistic information behind those seemingly indecipherable numbers.
Final Destination
So, what happens at the very end? At the top of the stack, after going through the last replicated transformer layer, we obtain a final token representation ht*(L) (where t* denotes the current prediction position) that is projected through a linear output layer followed by a softmax.
The linear layer produces unnormalized scores called logits, and the softmax converts these logits into next-token probabilities.
Logits computation:
\[
\text{logits}_j = W_{\text{vocab}, j} \cdot h_{t^*}^{(L)} + b_j
\]
Applying softmax to calculate normalized probabilities:
\[
\text{softmax}(\text{logits})_j = \frac{\exp(\text{logits}_j)}{\sum_{k} \exp(\text{logits}_k)}
\]
Using softmax outputs as next-token probabilities:
\[
P(\text{token} = j) = \text{softmax}(\text{logits})_j
\]
These probabilities are calculated for all possible tokens in the vocabulary. The next token to be generated by the LLM is then selected — often the one with the highest probability, though sampling-based decoding strategies are also common.
Journey’s End
This article took a journey, with a gentle level of technical detail, through the transformer architecture to provide a general understanding of what happens to the text that is provided to an LLM — the most prominent model based on a transformer architecture — and how this text is processed and transformed inside the model at the token level to finally turn into a model’s output: the next word to generate.
We hope you have enjoyed our travels together, and we look forward to the opportunity to embark upon another in the near future.