This article shows how Shannon’s information theory connects to the tools you’ll find in modern machine learning. We’ll address entropy and information gain, then move to cross-entropy, KL divergence, and the methods used in today’s generative learning systems.
Here’s what’s ahead:
- Shannon’s core idea of quantifying information and uncertainty (bits) and why rare events carry more information
- The progression from entropy → information gain/mutual information → cross-entropy and KL divergence
- How these ideas show up in practice: decision trees, feature selection, classification losses, variational methods, and InfoGAN

From Shannon to Modern AI: A Complete Information Theory Guide for Machine Learning
Image by Author
In 1948, Claude Shannon published a paper that changed how we think about information forever. His mathematical framework for quantifying uncertainty and surprise became the foundation for everything from data compression to the loss functions that train today’s neural networks.
Information theory gives you the mathematical tools to measure and work with uncertainty in data. When you select features for a model, optimize a neural network, or build a decision tree, you’re applying principles Shannon developed over 75 years ago. This guide connects Shannon’s original insights to the information theory concepts you use in machine learning today.
What Shannon Discovered
Shannon’s breakthrough was to treat information as something you could actually measure. Before 1948, information was qualitative — you either had it or you didn’t. Shannon showed that information could be quantified mathematically by looking at uncertainty and surprise.
The fundamental principle is elegant: rare events carry more information than common events. Learning that it rained in the desert tells you more than learning the sun rose this morning. This relationship between probability and information content became the foundation for measuring uncertainty in data.
Shannon captured this relationship in a simple mathematical formula:
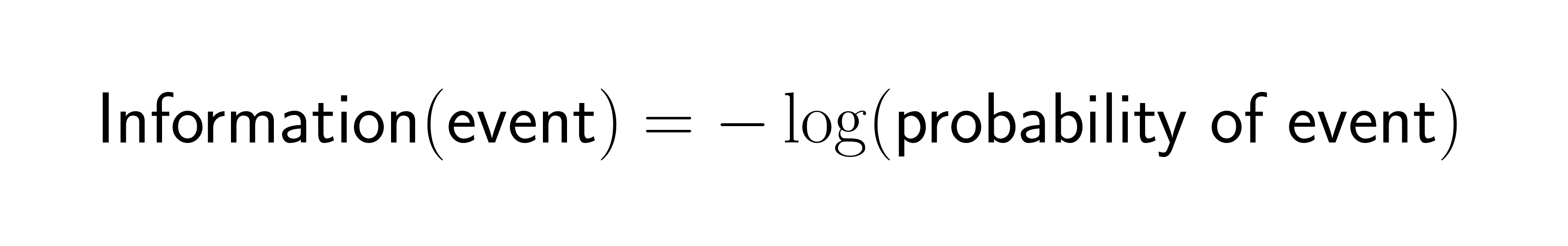
When an event has probability 1.0 (certainty), it gives you zero information. When an event is extremely rare, it provides high information content. This inverse relationship drives most information theory applications in machine learning.
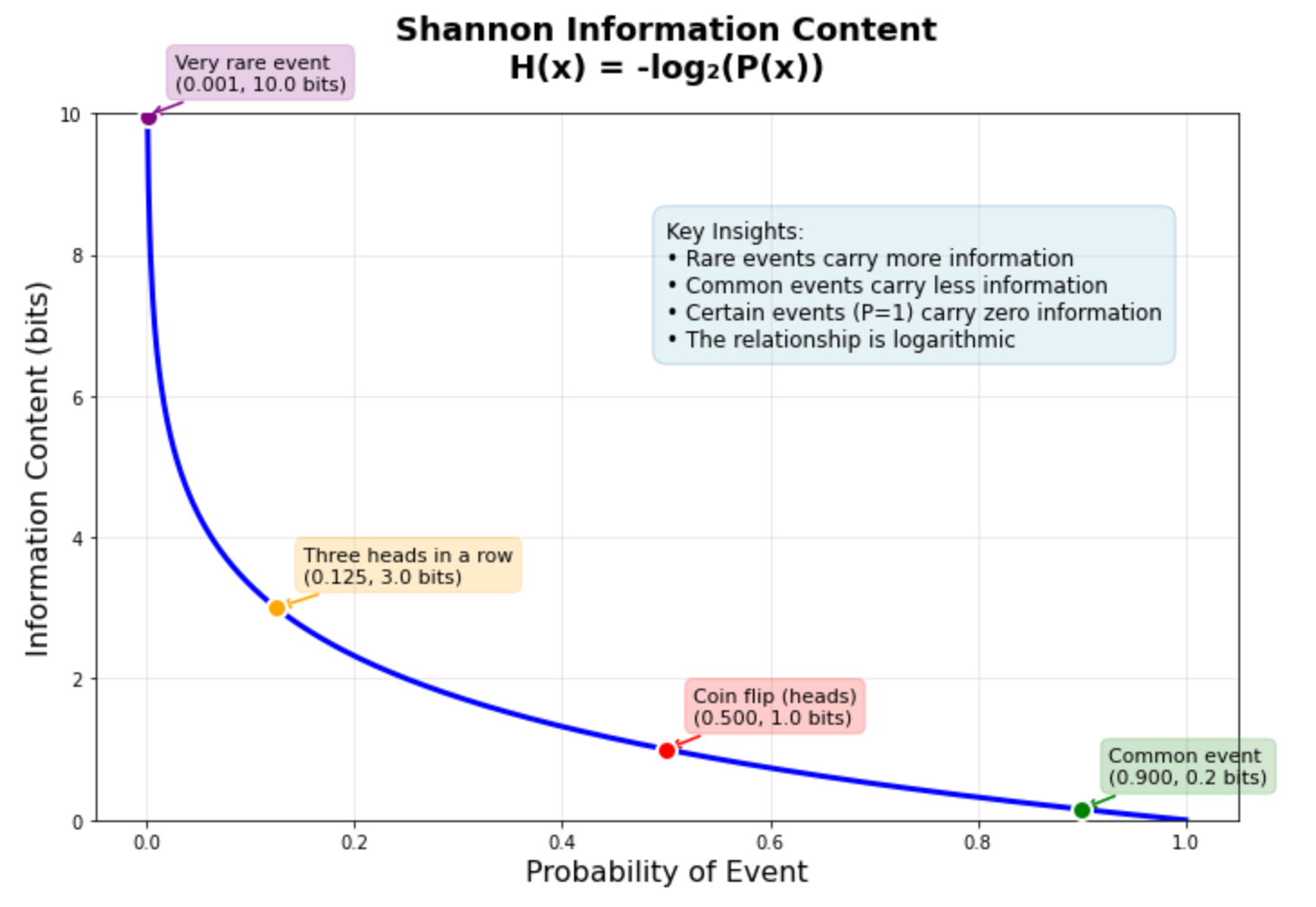
The graph above shows this relationship in action. A coin flip (50% probability) carries exactly 1 bit of information. Getting three heads in a row (12.5% probability) carries 3 bits. A very rare event with 0.1% probability carries about 10 bits — roughly ten times more information than the coin flip. This logarithmic relationship helps explain why machine learning models often struggle with rare events: they carry so much information that the model needs many examples to learn reliable patterns.
Building the Mathematical Foundation: Entropy
Shannon extended his information concept to entire probability distributions through entropy. Entropy measures the expected information content when sampling from a probability distribution.
For a distribution with equally likely outcomes, entropy reaches its maximum — there’s high uncertainty about which event will occur. For skewed distributions where one outcome dominates, entropy is lower because the dominant outcome is predictable.
This applies directly to machine learning datasets. A perfectly balanced binary classification dataset has maximum entropy, while an imbalanced dataset has lower entropy because one class is more predictable than the other.
For the complete mathematical derivation, step-by-step calculations, and Python implementations, see A Gentle Introduction to Information Entropy. This tutorial provides worked examples and implementations from scratch.
From Entropy to Information Gain
Shannon’s entropy concept leads naturally to information gain, which measures how much uncertainty decreases when you learn something new. Information gain calculates the reduction in entropy when you split data according to some criterion.
This principle drives decision tree algorithms. When building a decision tree, algorithms like ID3 and CART evaluate potential splits by calculating information gain. The split that gives you the biggest reduction in uncertainty gets selected.
Information gain also extends to feature selection through mutual information. Mutual information measures how much knowing one variable tells you about another variable. Features with high mutual information relative to the target variable are more informative for prediction tasks.
The mathematical relationship between entropy, information gain, and mutual information, along with worked examples and Python code, is explained in detail in Information Gain and Mutual Information for Machine Learning. This tutorial provides step-by-step calculations showing exactly how information gain guides decision tree splitting.
Cross-Entropy As a Loss Function
Shannon’s information theory concepts found direct application in machine learning through cross-entropy loss functions. Cross-entropy measures the difference between predicted probability distributions and true distributions.
When training classification models, cross-entropy loss quantifies how much information is lost when using predicted probabilities instead of true probabilities. Models that predict probability distributions closer to the true distribution have lower cross-entropy loss.
This connection between information theory and loss functions isn’t coincidental. Cross-entropy loss emerges naturally from maximum likelihood estimation, which seeks to find model parameters that make the observed data most probable under the model.
Cross-entropy became the standard loss function for classification tasks because it provides strong gradients when predictions are confident but wrong, helping models learn faster. The mathematical foundations, implementation details, and relationship to information theory are covered thoroughly in A Gentle Introduction to Cross-Entropy for Machine Learning.
Measuring Distribution Differences: KL Divergence
Building on cross-entropy concepts, the Kullback-Leibler (KL) divergence gives you a way to measure how much one probability distribution differs from another. KL divergence quantifies the additional information needed to represent data using an approximate distribution instead of the true distribution.
Unlike cross-entropy, which measures coding cost relative to the true distribution, KL divergence measures the extra information cost of using an imperfect model. This makes KL divergence particularly useful for comparing models or measuring how well one distribution approximates another.
KL divergence appears throughout machine learning in variational inference, generative models, and regularization techniques. It provides a principled way to penalize models that deviate too far from prior beliefs or reference distributions.
The mathematical foundations of KL divergence, its relationship to cross-entropy and entropy, plus implementation examples are detailed in How to Calculate the KL Divergence for Machine Learning. This tutorial also covers the related Jensen-Shannon divergence and shows how to implement both measures in Python.
Information Theory in Modern AI
Modern AI applications extend Shannon’s principles in sophisticated ways. Generative adversarial networks (GANs) use information theory concepts to learn data distributions, with discriminators performing information-theoretic comparisons between real and generated data.
The Information Maximizing GAN (InfoGAN) explicitly incorporates mutual information into the training objective. By maximizing mutual information between latent codes and generated images, InfoGAN learns disentangled representations where different latent variables control different aspects of generated images.
Transformer architectures, the foundation of modern language models, can be understood through information theory lenses. Attention mechanisms route information based on relevance, and the training process learns to compress and transform information across layers.
Information bottleneck theory provides another modern perspective, suggesting that neural networks learn by compressing inputs while preserving information relevant to the task. This view helps explain why deep networks generalize well despite their high capacity.
A complete implementation of InfoGAN with detailed explanations of how mutual information is incorporated into GAN training is provided in How to Develop an Information Maximizing GAN (InfoGAN) in Keras.
Building Your Information Theory Toolkit
Understanding when to apply different information theory concepts improves your machine learning practice. Here’s a framework for choosing the right tool:
Use entropy when you need to measure uncertainty in a single distribution. This helps evaluate dataset balance, assess prediction confidence, or design regularization terms that encourage diverse outputs.
Use information gain or mutual information when selecting features or building decision trees. These measures identify which variables give you the most information about your target variable.
Use cross-entropy when training classification models. Cross-entropy loss provides good gradients and connects directly to maximum likelihood estimation principles.
Use KL divergence when comparing probability distributions or implementing variational methods. KL divergence measures distribution differences in a principled way that respects the probabilistic structure of your problem.
Use advanced applications like InfoGAN when you need to learn structured representations or want explicit control over information flow in generative models.
This progression moves from measuring uncertainty in data (entropy) to optimizing models (cross-entropy). Advanced applications include comparing distributions (KL divergence) and learning structured representations (InfoGAN).
Next Steps
The five tutorials linked throughout this guide provide comprehensive coverage of information theory for machine learning. They progress from basic entropy concepts through applications to advanced techniques like InfoGAN.
Start with the entropy tutorial to build intuition for information content and uncertainty measurement. Move through information gain and mutual information to understand feature selection and decision trees. Study cross-entropy to understand modern loss functions, then explore KL divergence for distribution comparisons. Finally, examine InfoGAN to see how information theory principles apply to generative models.
Each tutorial includes complete Python implementations, worked examples, and applications. Together, they give you a complete foundation for applying information theory concepts in your machine learning projects.
Shannon’s 1948 insights continue to drive innovations in artificial intelligence. Understanding these principles and their modern applications gives you access to a mathematical framework that explains why many machine learning techniques work and how to apply them more effectively.
