A Gentle Introduction to Graph Neural Networks in Python
Introduction
Graph neural networks (GNNs) can be pictured as a special class of neural network models where data are structured as graphs — both training data used to train the model and real-world data used for inference — rather than fixed-size vectors or grids like image, sequences, or instances of tabular data.
While conventional neural network architectures like feed-forward models excel in modeling predictive problems like classification on structured, tabular data or images, GNNs are designed to accommodate problems where the relationships between data entities are complex and irregular. Take for instance social networks, molecular structures, and knowledge graphs. Like in any graph, the input data used for training and inference in GNNs is represented as a graph, with nodes representing entities (e.g. users in a social network) and edges representing relationships (e.g. friendships or follows between users).
Interested in better understanding how GNNs work through a gentle practical example in Python? Then keep reading.
Defining a Graph Neural Network in Python
In this introductory example of building a GNN, we will consider a small graph dataset associated with a social media platform, where each node represents a person and each edge connecting any two nodes is a friendship between persons. Furthermore, each node (person) has associated features like the person’s age, their interests, etc.
The target task of the GNN we will build is classifying people on either popular or not popular in the social network (binary classification), depending on whether having more than two or less than two friends in it, and taking into account:
- The person’s features, such as their interests
- The person’s connections with other persons
Therefore, GNNs give an extra layer of sophistication to predictive tasks, because they not only look at the target instance’s features to make a prediction but also at its relationship with other data instances, unlike classical classification and regression models.
Without further ado, let’s start coding. We’ll use several PyTorch components suitable for building GNNs, so we start by installing them first:
|
pip install torch pip install ogb pip install torch_geometric pip install networkx |
Now the necessary imports:
|
import os import torch import torch.nn.functional as F from torch_geometric.data import Data from torch_geometric.nn import GCNConv |
This is our “mini-social network” dataset or graph:
|
# Define graph dataset edge_index = torch.tensor([ [0, 1, 0, 2, 0, 4, 2, 4], [1, 0, 2, 0, 4, 0, 4, 2], ], dtype=torch.long) |
Basically, edge_index is a matrix of edges or connections between users. There are 5 users, numbered 0 to 4. The first connection is from user 0 to user 1, and we know this by looking at the first element in each row of the matrix. The second connection is the reciprocal of the previous one: user 1 to user 0. Then comes user 0 to user 2, and so on. User 3 seems not to be connected to anyone yet!
Now we model two numerical features for each person, in a tensor node_features: the person’s age, and their interest in sports, with 1 indicating interest and 0 indicating no interest.
|
# Define data features node_features = torch.tensor([ [25, 1], # Person 0 (25 years old, likes sports) [30, 0], # Person 1 (30 years old, does not like sports) [22, 1], # Person 2 (22 years old, likes sports) [35, 0], # Person 3 (35 years old, does not like sports) [27, 1], # Person 4 (27 years old, likes sports) ], dtype=torch.float) |
Visualizing a Graph Neural Network in Python
One way to visualize our graph neural network in Python can be accomplished by using the NetworkX library. It will create a graph from the edge list and Matplotlib to display it. An example of this is below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
import networkx as nx import matplotlib.pyplot as plt
# Convert the edge_index tensor to a list of edge tuples edge_list = edge_index.t().tolist()
# Create a NetworkX graph from the edge list G = nx.Graph() G.add_edges_from(edge_list)
# Optionally, include nodes that might be isolated (e.g., person 3) G.add_nodes_from(range(node_features.size(0)))
# Generate a layout for the nodes pos = nx.spring_layout(G, seed=42) # fixed seed for reproducibility
# Draw the graph with labels plt.figure(figsize=(6, 6)) nx.draw_networkx(G, pos, with_labels=True, node_color=‘lightblue’, edge_color=‘gray’, node_size=800) plt.title(“Visualization of the Social Network Graph”) plt.axis(‘off’) plt.show() |
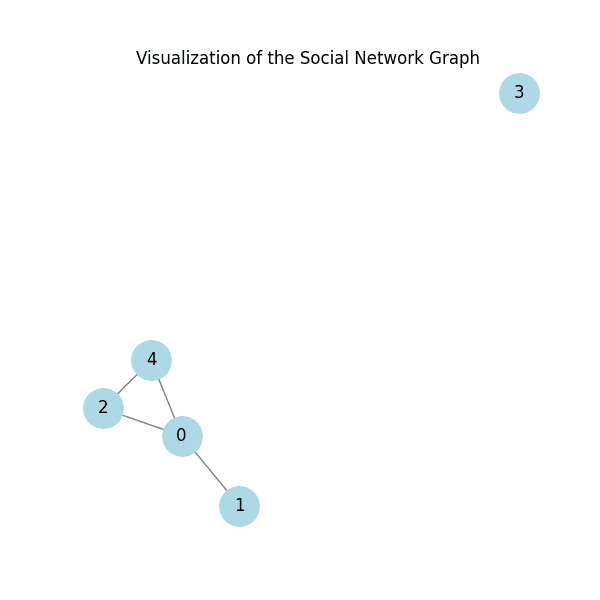
Figure 1: Visualization of the social network graph
Building a Graph Neural Network Model in Python
Now we define labels for the dataset of users, i.e. whether a person is popular or not, based on whether the person has more than 2 friends or not. The process entails calculating the number of friends of each person (ground truth) based on the adjacency matrix.
|
# Define dataset labels num_friends = torch.tensor([3, 1, 2, 0, 3]) labels = (num_friends >= 2).long() |
Using the following mask, we will indicate that the first three people will be used as training data to build the GNN, and the other two will be used later for inference. Finally, we also wrap everything into a Data object.
|
# Mask for separating training and testing data train_mask = torch.tensor([1, 1, 1, 0, 0], dtype=torch.bool) data = Data(x=node_features, edge_index=edge_index, y=labels, train_mask=train_mask) |
The next piece of code is crucial. It defines the GNN architecture and instantiates the model. In PyTorch, GNN models can be built by using graph convolutional layers, such as the ones implemented by the GCNConv class in torch_geometric.nn. Graph convolutional layers aggregate information from a node’s neighbors, helping learn representations that capture not only node features but also structural relationships in the graph.
|
# Define model class GNN(torch.nn.Module): def __init__(self, input_dim, hidden_dim, output_dim): super(GNN, self).__init__() self.conv1 = GCNConv(input_dim, hidden_dim) self.conv2 = GCNConv(hidden_dim, output_dim)
def forward(self, data): x, edge_index = data.x, data.edge_index x = self.conv1(x, edge_index) x = F.relu(x) # Activation function x = self.conv2(x, edge_index) return x
# Instantiate model model = GNN(input_dim=2, hidden_dim=4, output_dim=2) |
Training a Graph Neural Network in Python
The training model is reasonably similar to training other types of neural network models in PyTorch:
|
# Define optimizer optimizer = torch.optim.Adam(model.parameters(), lr=0.01)
# Train model for epoch in range(100): model.train() optimizer.zero_grad()
out = model(data) loss = F.cross_entropy(out[data.train_mask], data.y[data.train_mask])
loss.backward() optimizer.step()
if epoch % 10 == 0: print(f“Epoch {epoch}, Loss: {loss.item():.4f}”) |
Sample training output:
|
Epoch 0, Loss: 1.0987 Epoch 10, Loss: 0.8563 Epoch 20, Loss: 0.6542 Epoch 30, Loss: 0.5234 Epoch 40, Loss: 0.4231 Epoch 50, Loss: 0.3654 Epoch 60, Loss: 0.3120 Epoch 70, Loss: 0.2871 Epoch 80, Loss: 0.2654 Epoch 90, Loss: 0.2543 |
Graph Neural Network Inference in Python
Once the GNN has been trained, the inference process is straightforward. We pass the full dataset to calculate popularity predictions, including the two users that were not seen during training, and print the results. Notice that the argmax function is used to obtain the class with the highest probability for each user, from among the two available classes: this is the essence of binary classifiers like logistic regressors.
|
# Test model model.eval() with torch.no_grad(): predictions = model(data).argmax(dim=1)
print(“\nFinal Predictions (1=Popular, 0=Not Popular):”, predictions.tolist()) |
This is the resulting list of predictions:
|
# Test data inference output Final Predictions (1=Popular, 0=Not Popular): [1, 1, 1, 0, 1] |
So, we can see that all users are deemed popular except user 3, a.k.a. the “lonely user.”
Wrapping Up
To sum up, we have built a very simple GNN that uses a graph representation of a dataset to perform predictions based not only on the features of instances (represented by nodes) but also by looking at the relationships or connections with other instances.